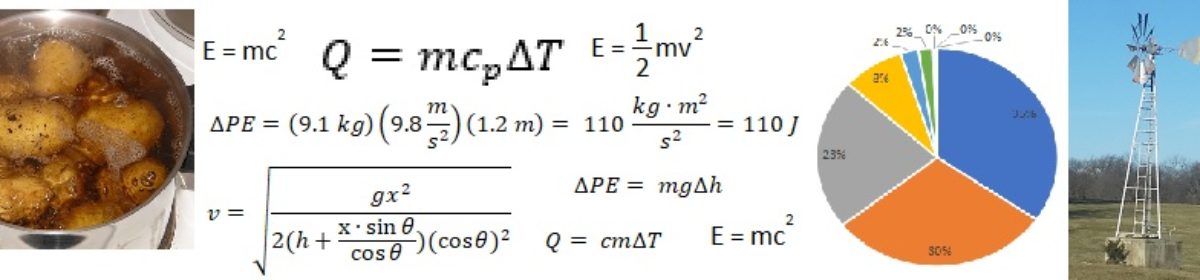Energy in Everyday Life – Thoughts on Energy

Melting Snow while Backpacking

Introduction

I enjoy backpacking in the great outdoors. As all good backpackers know, planning for access to water is a critical part of any backpacking trip. Backpacking is a lot of work and usually involves a lot of sweating, so keeping hydrated is necessary. However, maintaining a backpack as light as possible is also a key consideration, so one doesn’t want to carry a lot of water around. Thus, the usual strategy is to stay close to natural sources of water and bring a good water filter to allow for regular refills of water containers.

As a side note, how much work is a backpacking trip, you ask? Oh, at 100% efficiency, almost one million Joules worth of work would be required on a typical mountainous trail with about 1,000 meters of up and down (average 5% grade for a 20 kilometer, or about 12.5 mile, trip) during the full trip. (That calculation is simply the potential energy, which is the mass multiplied by acceleration due to gravity multiplied by the total elevation change). However, considering the body is probably only about 5% efficient in this case, the real energy use is approximately 20 million Joules, which is equivalent to a total of 5,000 food calories. That is just the extra calories of food energy “burned” during the trip in addition to the resting metabolic calorie burn of about 2,000 calories per day.

While on a backpacking trip some time ago, my brother and I took a day hike up a mountain and we knew we would not be near any sources of water for a good portion of the day. I had two water bottles with me on the backpacking trip, one un-insulated bottle and one insulated Thermos bottle. However, I didn’t have enough foresight to bring a smaller bag on the trip to carry around for the day hike, so all I had was a plastic grocery sack (I know, some Californians reading this post will cringe at those words), and thus I only took one of my water bottles. Unfortunately, it turned out that I selected the wrong water bottle to take with me.

You see, even though I tried to ration my water intake, I found I was out of water with several miles left to hike. Fortunately, we found some snow that I ate a good amount of, and also packed a good amount into my water bottle. I figured it could melt as we went along our merry way and I would soon have some nice cool water to drink. Well, that didn’t work out as well as I hoped because the snow was painfully slow to melt. Ironically, as we continued our hike, we ended up in a downpour that lasted a few hours. So I was soaked to the bone and dehydrated at the same time, and I still couldn’t get the darn snow to melt in my water bottle!

I had plenty of time during the hike to think about methods to melt the snow into water so I could drink it. Since it relates to energy, I thought I would share my findings here. The underlying assumption below is that conduction heat transfer through the insulated water bottle was negligibly low in the short term, which I think turned out to be a pretty good assumption. Also, a spreadsheet containing the calculations is available below.

Air Blowing Method

My first thought was to simply blow air into the water bottle’s straw and have it come out the little pressure release hole. It would work like any basic heat exchanger. I could transfer heat from the air I exhaled into the snow and cause it to melt. We should all be somewhat familiar with heat exchangers, as many of us have at least two in/near our dwelling places as part of an air conditioning system. One heat exchanger (located inside) allows the transfer of heat from the air inside the living space into a refrigerant, and the other heat exchanger (located outside) allows the transfer of heat from the refrigerant to the outside air.

We can use a simple equation to determine how much air I would need to blow through my water bottle straw to melt the snow. To formulate this equation, I simply use the fact that the amount of heat required to melt the snow must be the same as the amount of heat lost by the air as it travels through the snow in the bottle.

Where

Q is the total amount of heat required to be transferred from the air to the snow, in Joules.
is the total mass of air required, in kilograms.
is the specific heat of air, which is 1.0 Joules per kilogram degrees Celsius.
is the change in temperature experienced by the air as it moves from my mouth to the exit hole, in degrees Celsius. I assume the air temperature goes from about 32 degrees Celsius when it exits my mouth to about 5 degrees Celsius when it exits the water bottle, for a change in temperature of 27 degrees C.
is the total mass of snow, in kilograms. My water bottle fits about 0.5 liters of water. I haven’t packed the snow in completely tight, so I have about 0.4 liters of snow at a density of about 0.6 kilograms per liter, for a total of 0.24 kilograms of snow.
is the latent heat of fusion ((Wikipedia link)) of water, which is 334,000 Joules per kilogram.

Now all we need to do is solve for to obtain how much air it would take going through the “heat exchanger” to melt the snow. However, just knowing the total mass of air required is not very helpful. What I really want to know is how long it will take to get that mass of air through the water bottle. Thus, I need to know my respiration rate. I need to know how much air (in units of mass, or kg) I can blow through the bottle in a given amount of time. A typical adult respiration rate is about 6 liters of air per minute. However, when I am hiking with a backpack on I am exercising relatively vigorously, so I probably have a respiration rate around 50 liters per minute.

At an altitude of about 6,000 feet above sea level, the density of air is about 1.0 kilograms per liter. Using all of this information and solving for the time required to melt the snow (see the spreadsheet attached below if you want to follow all the math there), I obtain:

So it would take me about an hour to get enough air through the water bottle to melt the snow. However, this assumes that all of the air I exhale goes through the water bottle. I found that to be unsustainable in practice, as the water bottle restricted my exhalations enough that I would quickly run out of breath (remember, I am hiking on mountains wearing a 35-pound backpack). So I could really only get about one third of the air I exhaled through the water bottle. That results in about three hours to melt the snow. I am not that patient.

Potential Energy Input Method

My next thought was to use potential energy of the snow to melt it. The thought process is relatively simple. When I held the water bottle upright, there was a small pocket of air at the top. So if I turned the water bottle over, there would be stored potential energy in the lump of snow because the snow tended to stick to the bottom of the bottle.

As you will recall, potential energy is stored mechanical energy. In this case, it is the energy of the snow that can be realized as the snow falls the short distance from one end of the water bottle to the other. That potential energy must go somewhere as the snow falls. Initially, some energy becomes kinetic energy as the snow moves. When the snow stops against the bottom end of the bottle, about the only place for that energy to go is in the form of heat to the snow. Bingo! All I have to do is tip the water bottle upside-down enough times and I convert enough potential energy into heat energy to melt the snow!

So how many times do I need to invert the water bottle? Using the equation from the previous example, I already know it takes about 80,000 Joules of energy to melt the snow. So I just need to figure out the amount of potential energy for the snow in one time of inverting the water bottle.

It turns out the potential energy is about 0.1 Joules. So I only need to invert the water bottle 850,000 times. Assuming I can invert the water bottle once per second, this ends up being about 10 days. I am definitely not that patient.

Shaking Method

So what if I could speed up the potential energy process with some kinetic energy instead? Instead of inverting the bottle and waiting for the snow to fall in the water bottle, I can just orient the bottle horizontally and shake it back and forth instead and get a similar effect. I can increase the rate of impacts between the snow and the inside of the water bottle and maybe even increase the amount of heat added to the snow on each impact.

Consider the physics of what is going on inside the bottle as I shake it back and forth. As I shake the bottle in one direction, the bottle and snow move together. Then as I move the bottle in the other direction, the snow slams into one end of the bottle. This motion can be represented as a sinusoidal function. All I need to know are the amplitude of the motion and the period of the motion and I can fully describe the maximum velocity and acceleration of the motion. I assume the total range of motion is about 20 centimeters and I can move the bottle back and forth about three times per second. Thus, the motion of the bottle can be represented in this plot:

The position, velocity, and acceleration of the bottle can be represented by these equations (with just some calculus magic going on in the background):

In these equations, A is the amplitude of the motion, which is 10 centimeters, and T is the period of the motion, or the time it takes to complete a full cycle of motion, which is 0.333 seconds. The maximum velocity of the bottle (represented by the first portion of the velocity equation) is about 2 meters per second and the maximum acceleration (again, represented by the first portion of the acceleration equation) is about 35 meters per second squared, or about 3.5 times the acceleration of gravity. Considering a major league baseball pitcher can move a baseball from zero to 95 miles per hour in about 0.3 seconds (acceleration of about 15 times that of gravity), that seems like a reasonable value for acceleration.

It is the maximum velocity that I am interested in since that feeds into the calculation of kinetic energy for each cycle of bottle motion. It turns out that the kinetic energy in one impact of snow using the shaking method is about four and a half times the potential energy of the snow using the gravity method. In addition, the rate of impacts is about six times the rate for the gravity method. Thus, the shaking method is about 27 times as efficient as the gravity method. Still, it would take about nine hours to melt the snow using the shaking method, and that is assuming my arms don’t fall off before that point as a result of doing that much shaking. Nine hours is still too long.

Conclusions

In conclusion, none of the methods I tried turned out to be very effective for melting snow inside the insulated water bottle. The amount of time calculated for each method is shown in the table below. For comparison, I considered how long it would take the snow to melt if I had an uninsulated container sitting in room temperature (with heat transfer via convection of the surrounding air), using similar analysis to a previous post. It turned out that that method would actually result in a shorter time to melt the snow than any of the other methods.

So how did I end up melting the snow? The truth is, I never got the snow fully melted during the backpacking trip. When I found that the snow was not melting in spite of my best efforts, I decided to try another experiment. I decided to see how long it would take the snow to melt inside the bottle. Sure enough, when I arrived home approximately 24 hours after I put the snow in the bottle, there was still a small amount of snow remaining. So an insulated water bottle is pretty effective at keeping a drink cold. And if you are out backpacking and see some snow you want to use for drinking water, I recommend using a fire to melt it!

If you are interested in the calculations, see this spreadsheet:

Backpacking Snow Melting Calculations Download

Energy Comparison: Driving versus Vacuuming

Introduction

This post is a continuation of a previous post to answer an additional example of an energy comparison. This calculation, like the previous one, deals with energy use in everyday life. The question we will start with is:

What takes more energy, driving your car to the grocery store or vacuuming the floors in your entire house?

Of course, the first thing you should think is the answer to every science and engineering question there is: “it depends.” In this case, the answer depends on a number of related questions, possibly including these:

To which grocery store am I driving? The close one or the one across town or in the nearest bigger city?
Which car am I driving? The small one with good fuel economy or my gas-guzzling truck?
How thoroughly will I vacuum the floors? Just a quick job to pick up anything visible or a full and complete job going over every square inch multiple times?

So, we need to make some reasonable assumptions. And once again, as in the previous example, we need to take the time to think about what we are actually measuring: useful energy or total energy consumed. As mentioned in the previous post, the conversion of energy is never perfectly efficient. So when we talk about energy, we need to be careful and deliberate about what quantity we are actually measuring or calculating. Are we calculating the energy to perform a task in an ideal (imaginary) system or in the real world? In this case, we are calculating the amount of energy that is purchased, not the amount of useful energy that is used. Thus, we will calculate the amount of energy stored in the gasoline that is used in the vehicle on one hand and the amount of electrical energy that is consumed from the grid on the other hand.

I will point out here that my goal in this post and pretty much all of my posts is not necessarily coming up with exact answers to the questions posed. My goal is to compare, to prompt more thinking, to explore the topics, and to get approximate answers. We need to approach problems differently for different situations. When human lives depend on the answers (which happens regularly in engineering, by the way, for calculations like structural members for bridges), then exactness and accuracy matter. Such is not the case with my calculations here. We are just exploring.

Thus, I will make the following reasonable assumptions about driving to the grocery store (and back home again):

The distance to the grocery store is 8 kilometers (that is about 5 miles, which is just slightly under the average distance to the nearest Walmart of 6.7 miles as explained in this interesting paper).
Fuel economy of the vehicle is 10.5 kilometers per liter of gasoline (about 25 miles per gallon, which is approximately the average in America).
The energy density of gasoline is 45 megajoules per kilogram (MJ/kg).
Vehicle efficiency (converting the chemical energy stored in gasoline to useful energy moving the vehicle) is 20%.

I will then make the following assumptions about vacuuming the house:

The surface area of flooring in the house is 190 square meters (based on average figures of new homes built over the past 40 years being about 2,000 square feet).
Only the carpet gets vacuumed.
The ratio of carpet to total flooring is 60% (based on flooring sales figures in 2006 and 2016).
About 60% of the carpet surface gets vacuumed (typical routine vacuuming doesn’t cover under furniture, etc.).
The carpet gets vacuumed at a rate of 0.2 square meters (about two square feet) per second. This is perhaps the most subjective assumption in the entire analysis, but this seems to be a reasonable rate.
The vacuum cleaner uses 1,000 watts of power when on.

Calculations

We can express the total amount of energy consumed by the vehicle in the trip to the grocery store in equation form as:

Where

E equals total chemical energy stored in the gasoline that is consumed, in Joules.
D equals the distance to the store, in kilometers.
G equals the energy density of the gasoline, in joules per kilogram.
equals the mass density of the gasoline, in kilograms per liter.
F equals the fuel economy of the vehicle, in kilometers per liter.

Plugging in the numbers, we obtain the following:

Note that this is the actual energy consumed, not the useful energy. Gasoline-powered vehicles are typically about 20% efficient, so if you could calculate just the mechanical energy it would take to move the car to the grocery store and back, it would be about 5 million Joules instead of 25 million Joules. All that extra energy doesn’t do anything useful to move the car, but it is energy that the driver has to purchase in the form of gasoline.

Switching gears (pun intended), we can express the total amount of energy consumed during vacuuming of the house in equation form as:

Where

equals the total electrical energy removed from the grid by the vacuum, in Joules.
P equals the (average) electrical power consumed by the vacuum during vacuuming, in Watts.
T equals the time required to do the vacuuming, in seconds.

And

Where

equals the total floor area of the house, in square meters.
equals the fraction of total flooring in the house that is carpet, unitless.
equals the fraction of total carpet that gets vacuumed, also unitless.
R equals the rate of vacuuming, in square meters per second.

Plugging in the numbers, we obtain the following:

Conclusions

As is obvious from the results above, driving to the grocery store takes a lot more energy than vacuuming the entire house. In fact, it takes about 70 times as much energy to drive to the grocery store than it does to vacuum the entire house. Did you realize traveling by vehicle was so energy intensive?

Now, let’s look at comparing to some other household uses of energy. In a previous post, I looked at the energy to lift a bag of potatoes up to the counter (about 100 Joules) and the energy to heat up about one liter of water to boiling temperature (about 400,000 Joules). Now, before we make any comparisons, we must first realize that in the previous post I considered the ideal case. That is, the amount of energy consumed in a perfect system, with no energy losses due to inefficiency or friction or anything else. Conversely, in this post, I am considering the actual energy used, as in, the energy contained in the “fuel” that gets used up.

Without going into too much detail and specifics, I will simply assert that it takes about 500 Joules of energy purchased (in the form of food) to perform 100 Joules worth of work to lift the bag of potatoes up to the counter. The assumption here is that the human body is approximately 20% efficient at converting food energy into mechanical energy.

Similarly, it takes about 570,000 Joules of energy purchased (in the form of electricity or natural gas for the stove) to heat up a liter of water to boiling temperature. That is, I assume that the stove is approximately 70% efficient at converting electrical or chemical energy into heat energy in the target substance (the water). In this case, most of the energy loss occurs not in converting electrical or chemical energy into heat (assuming the stove is modern enough that combustion is pretty well complete) but in heat loss to the surrounding environment.

To summarize, it takes approximately the same amount of energy to vacuum the entire house as it does to bring a quart of water to a boil. It takes significantly less energy to lift a bag of potatoes, and significantly more energy to drive to the grocery store and back. For easy comparison, see the table below.

Also, feel free to look at the simple calculations on this spreadsheet:

Vacuuming-and-Driving-Calculations Download

Should I Leave the Milk Out?

Introduction

For someone like me who constantly thinks about energy, even getting cold cereal ready to eat in the morning can be a mind-engaging task. As I pull the milk out of the refrigerator to pour on my cold cereal, I know I will probably want the milk again after I finish my cereal in order to pour myself a bowl of fresh milk to finish off my breakfast. The question always pops into my head, “should I leave the milk out, or put it back in the fridge until I need it again?” Of course, the correct answer to this question is, it doesn’t really matter. But for an energy enthusiast like me, I want the real answer. The answer that involves the least amount of energy wasted.

To reiterate, the two options, with respect to what happens with the fridge and the milk, are:

Option A: Open fridge (assume the fridge is open for about 5 seconds each time it is opened) and take milk out, leave the milk on the counter for 15 minutes, and then open fridge to return the milk.
Option B: Open fridge, close fridge for about 15 seconds while pouring milk, open fridge again to return the milk; 15 minutes later, open the fridge again to get the milk out, close fridge for 15 seconds while pouring milk, open fridge to return the milk.

So, the way I see it, it comes down to which option wastes more energy. Both options involve some “waste” of energy from the fridge when the fridge is opened to remove and return the milk. The “extra” energy wasted in Option A is the loss of coldness of the milk sitting on the counter for 15 minutes, while the extra energy wasted in Option B is the extra loss of cold air from the fridge when it is opened two additional times. So we just need to calculate the wasted energy.

We will make some assumptions as we go through these calculations, and the answers will vary based on the assumptions we make and the uncertainty in the numbers we use. Keep in mind that for this particular problem, we aren’t really looking for exact answers, we are looking for good enough answers that will allow us to compare the two options. Do both options result in about the same energy waste, or is one of them substantially greater than the other?

Another thing to keep in mind is that we aren’t just looking for the answer to this specific question, we are thinking about how this answer will apply to similar situations. What if what we are removing from the fridge isn’t milk, but something else? What if we are removing something from the freezer instead of the fridge? What if that something is out for an hour instead of just 15 minutes?

While we perform our calculations and compare values, we are looking at the broader picture, for rules to govern our use of the refrigerator in general. Can we come up with some good general ground rules and energy estimates that will make our future use of the refrigerator as efficient as possible? That is the goal.

Picture of a refrigerator packed with various contents, including milk. — Opening the fridge is always an adventure…

Internet Research

Now, before we go performing a bunch of calculations, we will check to see what the Internet says about this energy efficiency question. The topic that usually comes up under any searches about whether I should leave the milk out is food safety. The standard answer for how long milk can be left out of a refrigerator without spoiling seems to be about two hours. However, some Europeans normally leave their milk out of the fridge due to a different pasteurization process, though the percentage of milk of this type of milk that is consumed varies from country to country.

But that isn’t what we are looking for about energy efficiency. It turns out there are some ideas out there about how long the refrigerator door should be left open, such as this insightful question and answer post. There are also plenty of general energy saving tips for refrigerators and other kitchen appliances, but they don’t generally get into the details of how long or how often doors should be left open.

Calculation for Option “A” Energy Wasted

So it looks like we will just have to calculate the answers and see how things turn out. In the calculations below, I am assuming a full or nearly full gallon of milk. Let’s start with the extra energy wasted in Option A: the energy wasted with the milk sitting out on the counter. When the milk container sits out for 15 minutes, there are four ways that heat is being transferred into the milk:

Convection heat transfer from the surrounding air,
Conduction heat transfer through the surface the container is sitting on,
Condensation of water vapor on the outside surface of the container, and
Radiation heat transfer from the surrounding environment.

A graphic depicting four mechanisms by which heat is transferred into the milk and container: convection, conduction, radiation, and condensation. — Four mechanisms by which heat is transferred into the milk and container.

It is instructive to first consider the total amount of heat transfer required to occur to bring the entire gallon of milk up to room temperature. To calculate this, we simply use the heat equation:

Heat equation: Q equals m c delta T. Heat energy equals mass multiplied by specific heat capacity multiplied by the temperature difference.

The specific heat capacity of milk is approximately 3,790 joules per kilogram degrees Celsius, and one gallon of milk has a mass of 3.8 kilograms. Thus, the heat required is:

We can expect the heat transferred in 15 minutes to come well short of this value, as we know by experience that it takes at least a few hours for milk to get even close to room temperature. In starting my heat transfer calculations, I can immediately discount the effect of radiation heat transfer, as I know it is relatively very small in cases with relatively minimal difference in temperature (which would include this case with only 20 degrees Celsius difference).

Thus, I start by calculating convection heat transfer. Convection heat transfer calculations get fairly involved, so I will spare you the gory details of a slew of dimensionless numbers (including the Prandtl number, the Grashof number, the Nusselt number, the Rayleigh number, the Biot number, and the Fourier number) and strange correlations (including raising a factor to the power of 8/27). If you are interested, though, you can see my spreadsheet with the calculations attached below.

Suffice it to say, a good estimate for heat added to the milk via convection during the 15 minutes sitting on the counter is about 15,000 joules.

I can now calculate the conduction through the surface. I do this by using equations that assume the surface that the milk is sitting on is a semi-infinite solid. This assumption is reasonable in some situations but not others. I could attempt to use finite element analysis and numerical methods to come up with better answers, but instead I am just going to use engineering judgment to modify the answers into something reasonable based on what I know about the scenario. Anyway, it turns out that it matters a great deal what material the surface is made of. The table below shows the calculated energy transfer due to heat conduction in 15 minutes for different surfaces, along with my values modified to be more realistic.

Table of energy values in joules for different counter surfaces: steel at approximately 22,000 joules, granite at 12,500 joules, wood at 3,000 joules, and hot pad at 900 joules.

As the calculation indicates, the heat loss when the milk is sitting on steel is much greater (over 150 times greater!) than the heat loss when the milk is sitting on a hot pad, towel, or equivalent insulator. My modifications to make the values more realistic are based on the fact that the materials are not actually semi-infinite (there is a limited volume of material for the heat to be transferred into, which is particularly significant for the steel surface) and to account for the thermal resistance of the milk container and its contact with the surface. At any rate, a reasonable average value for heat loss considering a wide variety of counter top surfaces is approximately 5,000 joules.

Next, I can calculate the heat added to the milk as a result of condensation. The energy transferred as a result of condensation is simply the latent heat of vaporization of the mass of water being condensed from water vapor into liquid water on the surface of the milk container. Of course, the amount of condensation will vary significantly depending on the humidity content of the air. I made some reasonable estimates of the amount of condensation that will occur in my calculations (see full details in spreadsheet attached below) and came up with a figure of approximately 5,000 joules of heat transfer due to condensation.

So, in summary, for Option A, the wasted energy is:

Table showing wasted energy via four heat transfer mechanisms: convection at 15,000 joules, conduction at 5,000 joules, condensation at 5,000 joules, radiation being negligible for a total of 25,000 joules.

In case you are interested, see attached file for details of heat transfer calculations for this section:

Milk Calculations Download

Calculation for Option “B” Energy Wasted

Next, we can calculate how much energy is “wasted” when the fridge is opened. The “waste” that occurs when a refrigerator is opened is a result of the cold air inside the fridge being replaced with room temperature air from outside the fridge. The total interior volume of a typical fridge is approximately 0.3 to 0.5 cubic meters. However, some of that volume is taken up by the contents of the fridge, so maybe a good average number for air volume of a fridge is 0.25 cubic meters. The mass of that air is simply:

Mass of air equals volume multiplied by density.

V is the volume of the air in the fridge and ρ is the density of the air, with a typical value being 1.2 kilograms per cubic meter. Thus, the mass of air in a fridge is about 0.3 kg. To calculate the energy required to cool this air from room temperature (about 22 degrees Celsius) to fridge temperature (about 2 degrees Celsius), as in the previous section, we simply use the heat equation:

The specific heat capacity of air is approximately 1000 joules per kilogram degrees Celsius. Thus, the heat required is:

Another factor to consider is the water vapor within the air that enters the fridge. While humidity levels in the fridge and in the air outside the fridge can vary significantly, let us examine a typical scenario just to get an idea.

Say the air in your home is at 50% relative humidity and the air in the fridge is at 100% relative humidity (not an uncommon situation if the fridge has been opened recently or if there is anything wet in the fridge). According to this chart, that would mean replacing air in the fridge with 0.005 pounds of water per pound of air with air from the room with 0.008 pounds of water per pound of air. This is an extra 0.003 pounds of water per pound of air. Since we have 0.3 kg of air, that means approximately one gram of extra water vapor in the fridge.

That small amount of water vapor doesn’t seem like a big deal. However, it takes a relatively large amount of energy to condense that one gram of water vapor, about 2,000 joules in fact. If the air in the house is hot and/or humid, the energy required to condense the additional water vapor can exceed the energy required to cool the air itself.

So all together, we can estimate that the energy “wasted” when the air in the fridge is replaced with room temperature air is approximately 10,000 joules. Of course, that represents the situation in which the entire volume of air from the fridge is totally replaced with room-temperature air. Since the fridge door is only open for 5-10 seconds, maybe only one quarter to one third of the air is replaced. So, we can estimate that one fridge door opening is approximately 3,000 joules of wasted energy. So two extra fridge door openings result in approximately 6,000 joules of wasted energy.

(Note that in our scenario, both extra door opening occur just 15 seconds or so after the previous opening, so much of the energy loss due to opening the door would have already occurred. That is, the air in the fridge is already somewhere between normal fridge temperature and room temperature. Thus, the amount of energy waste is actually some value lower than 6,000 joules for the two extra fridge openings, but the 6,000 joules is still a reasonable estimate.)

Conclusions

For the specific scenario postulated in the introduction, leaving the milk out of the fridge for 15 minutes wastes more energy than opening the fridge door two extra times to put the milk back and get it out again (25,000 joules compared to 6,000 joules).

If the period of time for the milk to be out was reduced to four minutes, it would be a close call as to which option would waste more energy (both options wasting about 6,000 joules in that case). So four minutes is probably a good cut-off time. If a full gallon of milk will be out for any longer than four minutes, it is better to just open the fridge and put it back in, then get it out again later.

I should note here that the energy waste we have discussed above is not the same as the extra electrical energy required to run the refrigerator. Refrigerators have a typical coefficient of performance of three to four, meaning that for every joule of electrical energy used by the refrigerator, three to four joules of heat energy can be removed from the interior of the fridge. So for scenario above with 6,000 joules of wasted energy, the fridge may use about 2,000 joules of electrical energy. That is about the energy required to power a 60-watt light bulb for about 30 seconds. (Yes, I realize most “60-watt” light bulbs do not actually take 60 watts of electricity to run anymore due to the efficiency of compact fluorescent and LED bulbs).

In the end, perhaps opening the door of the fridge isn’t as bad as we might think in terms of energy efficiency. Once the fridge has been open for a while, though, the cooling system will kick on and the cool air will mostly be wasted immediately to outside the fridge. Since a typical fridge cooling system uses 100-125 watts to run, it only takes about 30 seconds of the fridge running to remove the amount of heat equivalent to replacing all the room temperature air in the fridge with normal fridge temperature air. However, if the fridge is left open for a while, all of that 100-125 watts of the fridge running is almost immediately wasted as cold air flows right out the door.

I should also note that the amount of energy wasted by a refrigerator varies with the season of the year. In the winter time, when energy is being used to heat a home anyway, energy used by the fridge to cool the interior space is put out into the home as heat. So the energy isn’t really wasted at all. A person could, in fact, heat their home just by leaving the door of the refrigerator open all the time, but this isn’t really recommended (as the food wouldn’t stay cold and the fridge probably wouldn’t last long running all the time). Also, for those that have natural gas furnaces, using the furnace to heat the home is much more efficient than using electricity (such as using a refrigerator).

However, in the summer time, when air conditioning is on, the energy wasted by the fridge causes even more energy waste than just that used by the fridge itself. The air conditioning system must work to remove the heat energy (which has been converted from electrical energy by the fridge) from the home. So if you are going to pick a time of year when you are really strict about saving energy for the refrigerator, pick summer time.

Perhaps the most notable energy efficiency tips for use of a fridge that are not immediately obvious are the following:

There is value in keeping the air in the fridge dry by not leaving standing water or wet, uncovered foods because it takes a relatively large amount of energy to condense water (compared to the relatively small amount of energy to cool air).
When items are removed from the fridge, consider placing them on a hot pad or towel instead of directly on a counter or table surface (especially if that surface is metal!).

In conclusion, I hope this post has spurred some thoughts about energy efficiency for refrigerators. I hope I have answered the question “should I leave the milk out?” Of course, while each of us acting individually can’t save a whole lot of energy based on how we use our refrigerators, maybe if we all tried to be just a little more efficient, our combined efforts would add up to a big impact in terms of less waste and a better overall world environment. That is the dream, anyway.

And one final note. If you enjoyed this post, you might also enjoy a somewhat related post that answers the question of what appliance wins between a freezer and a toaster. Enjoy.