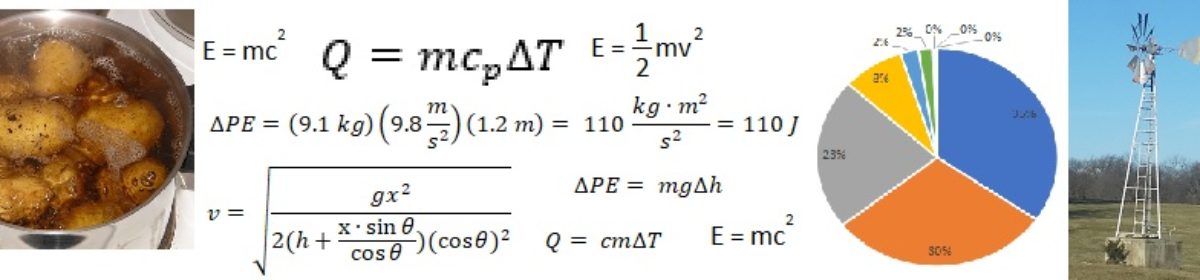Introduction
This post is a continuation of a previous post to answer an additional example of an energy comparison. This calculation, like the previous one, deals with energy use in everyday life. The question we will start with is:
- What takes more energy, driving your car to the grocery store or vacuuming the floors in your entire house?
Of course, the first thing you should think is the answer to every science and engineering question there is: “it depends.” In this case, the answer depends on a number of related questions, possibly including these:
- To which grocery store am I driving? The close one or the one across town or in the nearest bigger city?
- Which car am I driving? The small one with good fuel economy or my gas-guzzling truck?
- How thoroughly will I vacuum the floors? Just a quick job to pick up anything visible or a full and complete job going over every square inch multiple times?
So, we need to make some reasonable assumptions. And once again, as in the previous example, we need to take the time to think about what we are actually measuring: useful energy or total energy consumed. As mentioned in the previous post, the conversion of energy is never perfectly efficient. So when we talk about energy, we need to be careful and deliberate about what quantity we are actually measuring or calculating. Are we calculating the energy to perform a task in an ideal (imaginary) system or in the real world? In this case, we are calculating the amount of energy that is purchased, not the amount of useful energy that is used. Thus, we will calculate the amount of energy stored in the gasoline that is used in the vehicle on one hand and the amount of electrical energy that is consumed from the grid on the other hand.
I will point out here that my goal in this post and pretty much all of my posts is not necessarily coming up with exact answers to the questions posed. My goal is to compare, to prompt more thinking, to explore the topics, and to get approximate answers. We need to approach problems differently for different situations. When human lives depend on the answers (which happens regularly in engineering, by the way, for calculations like structural members for bridges), then exactness and accuracy matter. Such is not the case with my calculations here. We are just exploring.
Thus, I will make the following reasonable assumptions about driving to the grocery store (and back home again):
- The distance to the grocery store is 8 kilometers (that is about 5 miles, which is just slightly under the average distance to the nearest Walmart of 6.7 miles as explained in this interesting paper).
- Fuel economy of the vehicle is 10.5 kilometers per liter of gasoline (about 25 miles per gallon, which is approximately the average in America).
- The energy density of gasoline is 45 megajoules per kilogram (MJ/kg).
- Vehicle efficiency (converting the chemical energy stored in gasoline to useful energy moving the vehicle) is 20%.
I will then make the following assumptions about vacuuming the house:
- The surface area of flooring in the house is 190 square meters (based on average figures of new homes built over the past 40 years being about 2,000 square feet).
- Only the carpet gets vacuumed.
- The ratio of carpet to total flooring is 60% (based on flooring sales figures in 2006 and 2016).
- About 60% of the carpet surface gets vacuumed (typical routine vacuuming doesn’t cover under furniture, etc.).
- The carpet gets vacuumed at a rate of 0.2 square meters (about two square feet) per second. This is perhaps the most subjective assumption in the entire analysis, but this seems to be a reasonable rate.
- The vacuum cleaner uses 1,000 watts of power when on.
Calculations
We can express the total amount of energy consumed by the vehicle in the trip to the grocery store in equation form as:
Where
- E equals total chemical energy stored in the gasoline that is consumed, in Joules.
- D equals the distance to the store, in kilometers.
- G equals the energy density of the gasoline, in joules per kilogram.
equals the mass density of the gasoline, in kilograms per liter.- F equals the fuel economy of the vehicle, in kilometers per liter.
Plugging in the numbers, we obtain the following:
Note that this is the actual energy consumed, not the useful energy. Gasoline-powered vehicles are typically about 20% efficient, so if you could calculate just the mechanical energy it would take to move the car to the grocery store and back, it would be about 5 million Joules instead of 25 million Joules. All that extra energy doesn’t do anything useful to move the car, but it is energy that the driver has to purchase in the form of gasoline.
Switching gears (pun intended), we can express the total amount of energy consumed during vacuuming of the house in equation form as:
Where
equals the total electrical energy removed from the grid by the vacuum, in Joules.- P equals the (average) electrical power consumed by the vacuum during vacuuming, in Watts.
- T equals the time required to do the vacuuming, in seconds.
And
Where
equals the total floor area of the house, in square meters.
equals the fraction of total flooring in the house that is carpet, unitless.
equals the fraction of total carpet that gets vacuumed, also unitless.- R equals the rate of vacuuming, in square meters per second.
Plugging in the numbers, we obtain the following:
Conclusions
As is obvious from the results above, driving to the grocery store takes a lot more energy than vacuuming the entire house. In fact, it takes about 70 times as much energy to drive to the grocery store than it does to vacuum the entire house. Did you realize traveling by vehicle was so energy intensive?
Now, let’s look at comparing to some other household uses of energy. In a previous post, I looked at the energy to lift a bag of potatoes up to the counter (about 100 Joules) and the energy to heat up about one liter of water to boiling temperature (about 400,000 Joules). Now, before we make any comparisons, we must first realize that in the previous post I considered the ideal case. That is, the amount of energy consumed in a perfect system, with no energy losses due to inefficiency or friction or anything else. Conversely, in this post, I am considering the actual energy used, as in, the energy contained in the “fuel” that gets used up.
Without going into too much detail and specifics, I will simply assert that it takes about 500 Joules of energy purchased (in the form of food) to perform 100 Joules worth of work to lift the bag of potatoes up to the counter. The assumption here is that the human body is approximately 20% efficient at converting food energy into mechanical energy.
Similarly, it takes about 570,000 Joules of energy purchased (in the form of electricity or natural gas for the stove) to heat up a liter of water to boiling temperature. That is, I assume that the stove is approximately 70% efficient at converting electrical or chemical energy into heat energy in the target substance (the water). In this case, most of the energy loss occurs not in converting electrical or chemical energy into heat (assuming the stove is modern enough that combustion is pretty well complete) but in heat loss to the surrounding environment.
To summarize, it takes approximately the same amount of energy to vacuum the entire house as it does to bring a quart of water to a boil. It takes significantly less energy to lift a bag of potatoes, and significantly more energy to drive to the grocery store and back. For easy comparison, see the table below.
Also, feel free to look at the simple calculations on this spreadsheet: